In a previous post, we covered how to use Latent Growth Modeling in R to examine change in time. In that post, we assumed a simple linear model, which is often unrealistic. Here, I am going to show how we can free this assumption and find the best way to treat change in time.
We can use exploratory analysis and previous research to understand how to model change in time. Moreover, we can also compare models that treat change in time in different ways to find the best fit for our data.
If we look again at the log income in the Understanding Society data, we get this graph (see previous post for an explanation of the data and how it is structured):
ggplot(usl, aes(wave, logincome, group = pidp)) +
geom_line(alpha = 0.01) + # add individual line with transparency
stat_summary( # add average line
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "red"
) +
theme_bw() + # nice theme
labs(x = "Wave", y = "Logincome") # nice labels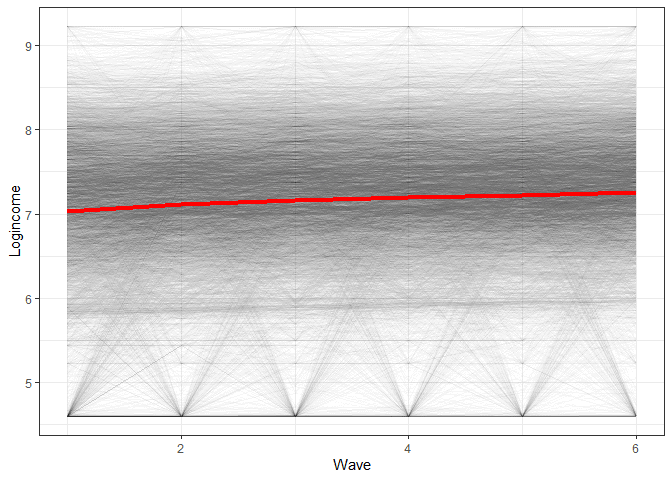
The graph would indicate we have an average change that is overall linear with a slight downward bend.
To see the individual level change, I also sampled 20 individuals and plotted each one’s change in income.
# sample 20 ids people <- unique(usl$pidp) %>% sample(20) # do separate graph for each individual usl %>% filter(pidp %in% people) %>% # filter only sampled cases ggplot(aes(wave, logincome, group = 1)) + geom_line() + facet_wrap(~pidp) + # a graph for each individual theme_bw() + # nice theme labs(x = "Wave", y = "Logincome") # nice labels
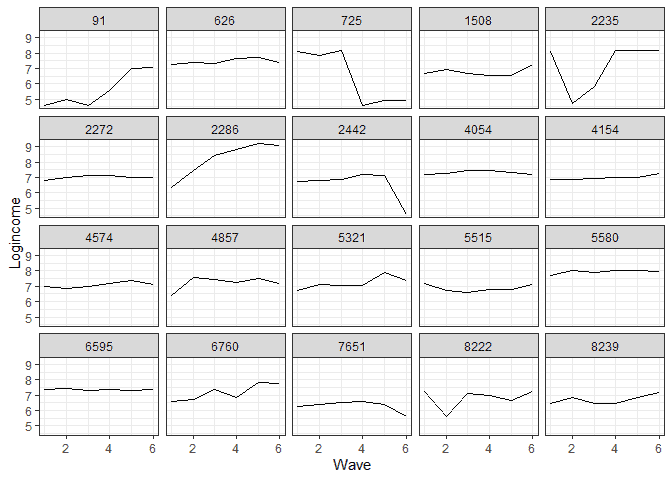
It appears that at the individual level, we have a more mixed bag, although linear change would not be a bad approximation for quite a few people.
Keeping this in mind, we can also decide on the best way to model change in time by comparing several different models and seeing which fits the data best. As a starting point, we can run the linear model, which will be our reference (see previous post for an explanation of the model and syntax):
library(tidyverse)
library(lavaan)
# first LGM
model <- 'i =~ 1*logincome_1 + 1*logincome_2 + 1*logincome_3 +
1*logincome_4 + 1*logincome_5 + 1*logincome_6
s =~ 0*logincome_1 + 1*logincome_2 + 2*logincome_3 +
3*logincome_4 + 4*logincome_5 + 5*logincome_6'
fit1 <- growth(model, data = usw)
summary(fit1, standardized = TRUE)
## lavaan 0.6-8 ended normally after 45 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 11
##
## Number of observations 8752
##
## Model Test User Model:
##
## Test statistic 523.408
## Degrees of freedom 16
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## logincome_1 1.000 0.827 0.842
## logincome_2 1.000 0.827 0.923
## logincome_3 1.000 0.827 0.949
## logincome_4 1.000 0.827 0.977
## logincome_5 1.000 0.827 0.993
## logincome_6 1.000 0.827 0.949
## s =~
## logincome_1 0.000 0.000 0.000
## logincome_2 1.000 0.115 0.128
## logincome_3 2.000 0.229 0.263
## logincome_4 3.000 0.344 0.406
## logincome_5 4.000 0.459 0.551
## logincome_6 5.000 0.574 0.658
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -0.047 0.002 -25.789 0.000 -0.497 -0.497
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.000 0.000 0.000
## .logincome_2 0.000 0.000 0.000
## .logincome_3 0.000 0.000 0.000
## .logincome_4 0.000 0.000 0.000
## .logincome_5 0.000 0.000 0.000
## .logincome_6 0.000 0.000 0.000
## i 7.063 0.010 734.511 0.000 8.538 8.538
## s 0.041 0.002 23.527 0.000 0.354 0.354
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.280 0.006 45.748 0.000 0.280 0.291
## .logincome_2 0.201 0.004 48.502 0.000 0.201 0.250
## .logincome_3 0.212 0.004 54.736 0.000 0.212 0.279
## .logincome_4 0.197 0.004 54.733 0.000 0.197 0.275
## .logincome_5 0.176 0.004 49.002 0.000 0.176 0.254
## .logincome_6 0.217 0.005 43.584 0.000 0.217 0.286
## i 0.684 0.012 55.548 0.000 1.000 1.000
## s 0.013 0.000 31.248 0.000 1.000 1.000Based on this model, log income is, on average, around 7.063 (~ £1,168) at the start of the study and goes up by 0.041 each wave (for more on the interpretation, see the previous post).
We can also visualize the change in time based on our model (again, check the previous post for explanations).
# predict the two latent variables
pred_lgm <- predict(fit1)
# create long data for each individual
pred_lgm_long <- map(0:5, # loop over time
function(x) pred_lgm[, 1] + x * pred_lgm[, 2]) %>%
reduce(cbind) %>% # bring together the wave predictions
as.data.frame() %>% # make data frame
setNames(str_c("Wave ", 1:6)) %>% # give names to variables
mutate(id = row_number()) %>% # make unique id
gather(-id, key = wave, value = pred) # make long format
# make graph (takes a minute to plot)
pred_lgm_long %>%
ggplot(aes(wave, pred, group = id)) + # what variables to plot?
geom_line(alpha = 0.01) + # add a transparent line for each person
stat_summary( # add average line
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "red"
) +
theme_bw() + # makes graph look nicer
labs(y = "logincome", # labels
x = "Wave")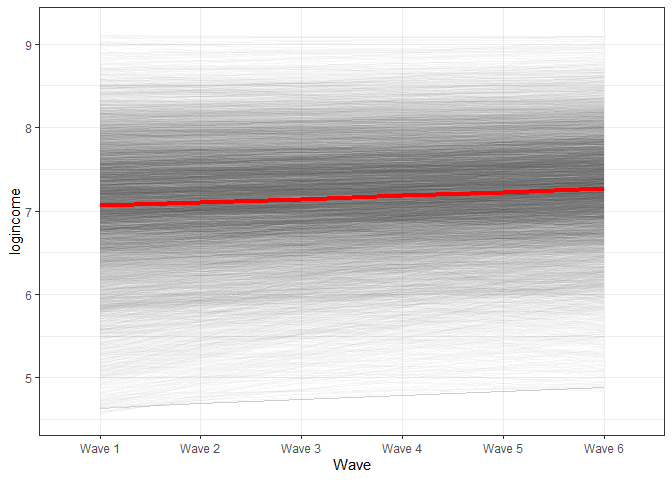
There are two general ways to expand this model to include non-linear change. One is by including polynomials while the other is by looking at relative change in time. We will cover both below.
Estimating non-linear LGM using polynomials
Including polynomials to model nonlinear effects has a similar motivation to regression modelling. A polynomial (or interaction) allows the effect to change depending on the values of a predictor. In the case of LGM, this would mean that we allow the slope to be higher or lower as time passes. This, in effect, would bend the trend upwards or downwards. If we want to allow for multiple bends, then we need to include multiple polynomials. Below, we will include just the square effects modelled as a latent variable “q” (but the model can be easily expanded to include cubed effects and so on).
# square LGM
model <- 'i =~ 1*logincome_1 + 1*logincome_2 + 1*logincome_3 +
1*logincome_4 + 1*logincome_5 + 1*logincome_6
s =~ 0*logincome_1 + 1*logincome_2 + 2*logincome_3 +
3*logincome_4 + 4*logincome_5 + 5*logincome_6
q =~ 0*logincome_1 + 1*logincome_2 + 4*logincome_3 +
9*logincome_4 + 16*logincome_5 + 25*logincome_6'
fit2 <- growth(model, data = usw)
summary(fit2, standardized = TRUE)
## lavaan 0.6-8 ended normally after 93 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 15
##
## Number of observations 8752
##
## Model Test User Model:
##
## Test statistic 168.391
## Degrees of freedom 12
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## logincome_1 1.000 0.843 0.877
## logincome_2 1.000 0.843 0.930
## logincome_3 1.000 0.843 0.956
## logincome_4 1.000 0.843 0.985
## logincome_5 1.000 0.843 1.002
## logincome_6 1.000 0.843 0.991
## s =~
## logincome_1 0.000 0.000 0.000
## logincome_2 1.000 0.271 0.299
## logincome_3 2.000 0.541 0.614
## logincome_4 3.000 0.812 0.949
## logincome_5 4.000 1.082 1.287
## logincome_6 5.000 1.353 1.590
## q =~
## logincome_1 0.000 0.000 0.000
## logincome_2 1.000 0.046 0.051
## logincome_3 4.000 0.185 0.210
## logincome_4 9.000 0.417 0.487
## logincome_5 16.000 0.741 0.881
## logincome_6 25.000 1.158 1.361
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -0.080 0.006 -12.637 0.000 -0.351 -0.351
## q 0.005 0.001 5.051 0.000 0.136 0.136
## s ~~
## q -0.011 0.001 -14.993 0.000 -0.893 -0.893
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.000 0.000 0.000
## .logincome_2 0.000 0.000 0.000
## .logincome_3 0.000 0.000 0.000
## .logincome_4 0.000 0.000 0.000
## .logincome_5 0.000 0.000 0.000
## .logincome_6 0.000 0.000 0.000
## i 7.039 0.010 701.030 0.000 8.354 8.354
## s 0.071 0.005 14.233 0.000 0.261 0.261
## q -0.006 0.001 -6.317 0.000 -0.124 -0.124
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.213 0.008 26.812 0.000 0.213 0.231
## .logincome_2 0.207 0.004 49.387 0.000 0.207 0.252
## .logincome_3 0.196 0.004 50.313 0.000 0.196 0.253
## .logincome_4 0.178 0.004 48.924 0.000 0.178 0.243
## .logincome_5 0.178 0.004 49.022 0.000 0.178 0.252
## .logincome_6 0.173 0.007 25.732 0.000 0.173 0.239
## i 0.710 0.014 49.658 0.000 1.000 1.000
## s 0.073 0.004 16.951 0.000 1.000 1.000
## q 0.002 0.000 15.218 0.000 1.000 1.000It appears that initially, log income goes up by 0.071 each wave, but as time passes, this bends downwards (because the square effect is negative) by 0.006 each wave. The variance of “q” (0.002) is the between variation in non-linear change. Substantively, it tells us if people have different non-linear bends in time. If this is 0, everyone follows the same non-linear trend. If the value is large, individuals are very different in the non-linear part of the change in time of income.
Next, we plot the new estimates of change from the new model. We will use a procedure similar to the one above. The main change is to the formula. Now, we need to add a new term, which is time squared (x^2) multiplied by the coefficient for the square effect (pred_lgm2[, 3]). We also added the line from the linear model for comparison.
# predict scores
pred_lgm2 <- predict(fit2)
# create long data for each individual
pred_lgm2_long <- map(0:5, # loop over time
function(x) pred_lgm2[, 1] +
x * pred_lgm2[, 2] +
x^2 * pred_lgm2[, 3]) %>%
reduce(cbind) %>% # bring together the wave predictions
as.data.frame() %>% # make data frame
setNames(str_c("Wave ", 1:6)) %>% # give names to variables
mutate(id = row_number()) %>% # make unique id
gather(-id, key = wave, value = pred) # make long format
# make graph
pred_lgm2_long %>%
ggplot(aes(wave, pred, group = id)) + # what variables to plot?
geom_line(alpha = 0.01) + # add a transparent line for each person
stat_summary( # add average line
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "blue"
) +
stat_summary(data = pred_lgm_long, # add average from linear model
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "red",
alpha = 0.5
) +
theme_bw() + # makes graph look nicer
labs(y = "logincome", # labels
x = "Wave")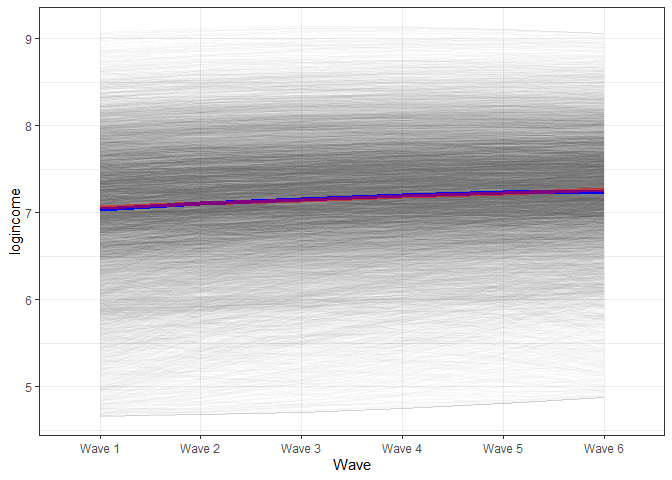
In the graph, we see that the blue line (based on the model with the squared effects) starts slightly below the red line, by the middle is slightly above and in the end, is somewhat lower. That being said, you need to squint your eyes to see a difference. While the square effects are significant, they might not be of substantive interest.
Non-linear change in time using relative change
The alternative way to model non-linear change is to estimate relative change. This is similar in spirit to including dummy variables in a regression model. The only thing we need to do is to tweak the loadings for the slope latent variable. We will fix only the first and last loading to 0 and 1. The rest of the loadings will not be fixed and will be estimated. Now, the interpretation of the slope will be the total amount of change from the first wave to the last one. The newly estimated loadings will tell us the proportion of change from the start until that point out of the total change observed.
# relative change LGM
model <- 'i =~ 1*logincome_1 + 1*logincome_2 + 1*logincome_3 +
1*logincome_4 + 1*logincome_5 + 1*logincome_6
s =~ 0*logincome_1 + logincome_2 + logincome_3 +
logincome_4 + logincome_5 + 1*logincome_6'
fit3 <- growth(model, data = usw)
summary(fit3, standardized = TRUE)
## lavaan 0.6-8 ended normally after 113 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 15
##
## Number of observations 8752
##
## Model Test User Model:
##
## Test statistic 413.271
## Degrees of freedom 12
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i =~
## logincome_1 1.000 0.821 0.838
## logincome_2 1.000 0.821 0.914
## logincome_3 1.000 0.821 0.939
## logincome_4 1.000 0.821 0.971
## logincome_5 1.000 0.821 0.988
## logincome_6 1.000 0.821 0.930
## s =~
## logincome_1 0.000 0.000 0.000
## logincome_2 0.158 0.023 6.977 0.000 0.081 0.091
## logincome_3 0.410 0.017 23.519 0.000 0.212 0.242
## logincome_4 0.718 0.017 43.392 0.000 0.370 0.438
## logincome_5 0.958 0.020 48.368 0.000 0.494 0.595
## logincome_6 1.000 0.516 0.585
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## i ~~
## s -0.202 0.011 -19.018 0.000 -0.477 -0.477
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.000 0.000 0.000
## .logincome_2 0.000 0.000 0.000
## .logincome_3 0.000 0.000 0.000
## .logincome_4 0.000 0.000 0.000
## .logincome_5 0.000 0.000 0.000
## .logincome_6 0.000 0.000 0.000
## i 7.070 0.010 719.672 0.000 8.616 8.616
## s 0.174 0.008 20.993 0.000 0.337 0.337
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .logincome_1 0.286 0.008 37.707 0.000 0.286 0.298
## .logincome_2 0.189 0.005 37.392 0.000 0.189 0.235
## .logincome_3 0.211 0.004 53.437 0.000 0.211 0.277
## .logincome_4 0.193 0.004 53.163 0.000 0.193 0.270
## .logincome_5 0.159 0.004 37.667 0.000 0.159 0.231
## .logincome_6 0.243 0.005 44.710 0.000 0.243 0.312
## i 0.673 0.013 50.205 0.000 1.000 1.000
## s 0.266 0.013 21.250 0.000 1.000 1.000So, based on these results from wave 1 to wave 6, income has increased, on average, by 0.174. If we had a genuinely linear change, we would expect the loadings to increase at the same rate of 0.2 per wave (five steps going from wave 1 to six out of a total change of 1 (the value of the last loading)). So the loading for “logincom_2” should be 0.2, the next, 0.4, and so on. We don’t see that. We see that the most change happened between waves 3 and 4. Then, around 30% of the total change happened ((0.718 – 0.410) * 100). On the other hand, very little change occurred between waves 5 and 6, less than 5%. This result would indicate that we don’t have linear change. We can visualize the change using a graph.
We need to extract the loadings to make a nice graph using the formula. We can use the parameterestimates() command to do that:
parameterestimates(fit3) ## lhs op rhs est se z pvalue ci.lower ci.upper ## 1 i =~ logincome_1 1.000 0.000 NA NA 1.000 1.000 ## 2 i =~ logincome_2 1.000 0.000 NA NA 1.000 1.000 ## 3 i =~ logincome_3 1.000 0.000 NA NA 1.000 1.000 ## 4 i =~ logincome_4 1.000 0.000 NA NA 1.000 1.000 ## 5 i =~ logincome_5 1.000 0.000 NA NA 1.000 1.000 ## 6 i =~ logincome_6 1.000 0.000 NA NA 1.000 1.000 ## 7 s =~ logincome_1 0.000 0.000 NA NA 0.000 0.000 ## 8 s =~ logincome_2 0.158 0.023 6.977 0 0.113 0.202 ## 9 s =~ logincome_3 0.410 0.017 23.519 0 0.376 0.444 ## 10 s =~ logincome_4 0.718 0.017 43.392 0 0.685 0.750 ## 11 s =~ logincome_5 0.958 0.020 48.368 0 0.919 0.996 ## 12 s =~ logincome_6 1.000 0.000 NA NA 1.000 1.000 ## 13 logincome_1 ~~ logincome_1 0.286 0.008 37.707 0 0.271 0.300 ## 14 logincome_2 ~~ logincome_2 0.189 0.005 37.392 0 0.180 0.199 ## 15 logincome_3 ~~ logincome_3 0.211 0.004 53.437 0 0.203 0.219 ## 16 logincome_4 ~~ logincome_4 0.193 0.004 53.163 0 0.186 0.200 ## 17 logincome_5 ~~ logincome_5 0.159 0.004 37.667 0 0.151 0.168 ## 18 logincome_6 ~~ logincome_6 0.243 0.005 44.710 0 0.232 0.253 ## 19 i ~~ i 0.673 0.013 50.205 0 0.647 0.700 ## 20 s ~~ s 0.266 0.013 21.250 0 0.242 0.291 ## 21 i ~~ s -0.202 0.011 -19.018 0 -0.223 -0.181 ## 22 logincome_1 ~1 0.000 0.000 NA NA 0.000 0.000 ## 23 logincome_2 ~1 0.000 0.000 NA NA 0.000 0.000 ## 24 logincome_3 ~1 0.000 0.000 NA NA 0.000 0.000 ## 25 logincome_4 ~1 0.000 0.000 NA NA 0.000 0.000 ## 26 logincome_5 ~1 0.000 0.000 NA NA 0.000 0.000 ## 27 logincome_6 ~1 0.000 0.000 NA NA 0.000 0.000 ## 28 i ~1 7.070 0.010 719.672 0 7.051 7.089 ## 29 s ~1 0.174 0.008 20.993 0 0.158 0.190
With some manipulation, we can extract just what we want:
# extract just th eloadings of the slopes loadings <- parameterestimates(fit3) %>% # get estimates filter(lhs == "s", op == "=~") %>% # filter the rows we want .[["est"]] # extract "est" variable # print result loadings ## [1] 0.0000000 0.1576471 0.4102628 0.7176219 0.9575655 1.0000000
We can follow a similar approach to the one before to create the long data with predicted scores from the LGM. The only difference is that we now loop over the loadings instead of the numbers 0 to 5:
# predict scores
pred_lgm3 <- predict(fit3)
# create long data for each individual
pred_lgm3_long <- map(loadings, # loop over time
function(x) pred_lgm3[, 1] +
x * pred_lgm3[, 2]) %>%
reduce(cbind) %>% # bring together the wave predictions
as.data.frame() %>% # make data frame
setNames(str_c("Wave ", 1:6)) %>% # give names to variables
mutate(id = row_number()) %>% # make unique id
gather(-id, key = wave, value = pred) # make long format
pred_lgm3_long %>%
ggplot(aes(wave, pred, group = id)) + # what variables to plot?
geom_line(alpha = 0.01) + # add a transparent line for each person
stat_summary( # add average line
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "green"
) +
stat_summary(data = pred_lgm_long, # add average from linear model
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "red",
alpha = 0.5
) +
stat_summary(data = pred_lgm2_long, # add average from squared model
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "blue",
alpha = 0.5
) +
theme_bw() + # makes graph look nicer
labs(y = "logincome", # labels
x = "Wave")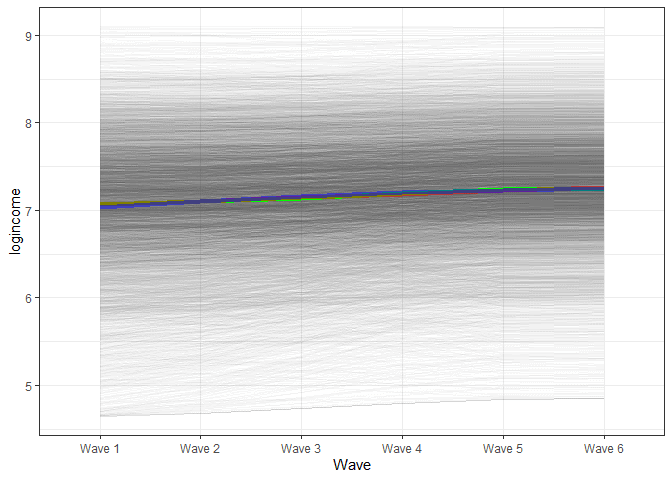
We see a very similar trend for the final model. It would appear that the trend here does not show a non-linear trajectory.
Finding the best fit
How do you decide on the best model? We can compare relative fit indices, like AIC and BIC, to help us with the decision (note that models are not nested, so can’t use the Chi-squared test):
anova(fit1, fit2, fit3) ## Chi-Squared Difference Test ## ## Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq) ## fit2 12 97516 97622 168.39 ## fit3 12 97761 97867 413.27 244.88 0 ## fit1 16 97863 97941 523.41 110.14 4 < 2.2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Based on AIC and BIC, the best-fitting model is the one with square effects. That being said, it’s always important to consider whether those effects are really important from a substantive point of view and whether using just a linear model would really lead to different conclusions.
Conclusions
Hopefully, that will give you an idea of how to estimate non-linear LGM, how to visualize this change, and how to interpret it. Visualizing these models is always helpful, as the interpretation can get quite tricky.
If you liked this, you could look at other blog posts, such as this introduction to multilevel modelling for longitudinal data or this one visualizing transition in time for categorical variables. You can also learn how to include time-constant and time-varying predictors in LGM models here and here.
Was the information useful?
Consider supporting the site:
