In a previous post, we introduced the multilevel model for change, a powerful model that can estimate change in time while separating within and between variation. While we discussed the basic model in detail, it can be expanded in several ways. Here, we will cover how to estimate non-linear change in time using the multilevel framework.
In the basic multilevel model for change, we have only one coefficient to describe the effect of time. This implies a stable or linear rate of change. In many applications, this is not an appropriate assumption, as rates of change can be different at different points in time. There are two main ways of modelling these non-linear trends: including polynomials and treating time as discrete.
Nonlinear change in time using polynomials
Let’s start with the first approach, including polynomials of time in the model. This is quickly done by creating new variables that take the values of time and square/cube/etc them. We will use as reference “wave0” which is a recoded version of time that starts from 0 (this is used to make the intercept easier to interpret, as discussed here).
usl <- mutate(usl,
wave0 = wave - 1,
wave_sq = wave0^2,
wave_cu = wave0^3)
select(usl, wave0, wave_sq, wave_cu) ## # A tibble: 52,512 × 3
## wave0 wave_sq wave_cu
## <dbl> <dbl> <dbl>
## 1 0 0 0
## 2 1 1 1
## 3 2 4 8
## 4 3 9 27
## 5 4 16 64
## 6 5 25 125
## 7 0 0 0
## 8 1 1 1
## 9 2 4 8
## 10 3 9 27
## # … with 52,502 more rowsBy including these new variables in a model, we allow for the effect of time to shift. When time has low values the main effect will have a large impact on the outcome, as time increases the square and the cube will become more and more important (due to their increased size). This allows for the rate of change to be different at different points in time. With the addition of each polynomial, we allow the change rate to “bend” once. If the effect of the polynomial is positive, the bend will be upwards, if it’s negative, it will bend downwards. The larger the size, the stronger the shift. Let’s look at an example. Below are the predicted scores for a hypothetical outcome where the main effect is 0. We see how the size of the outcome changes in time non-linearly due to the impact of the square estimate:
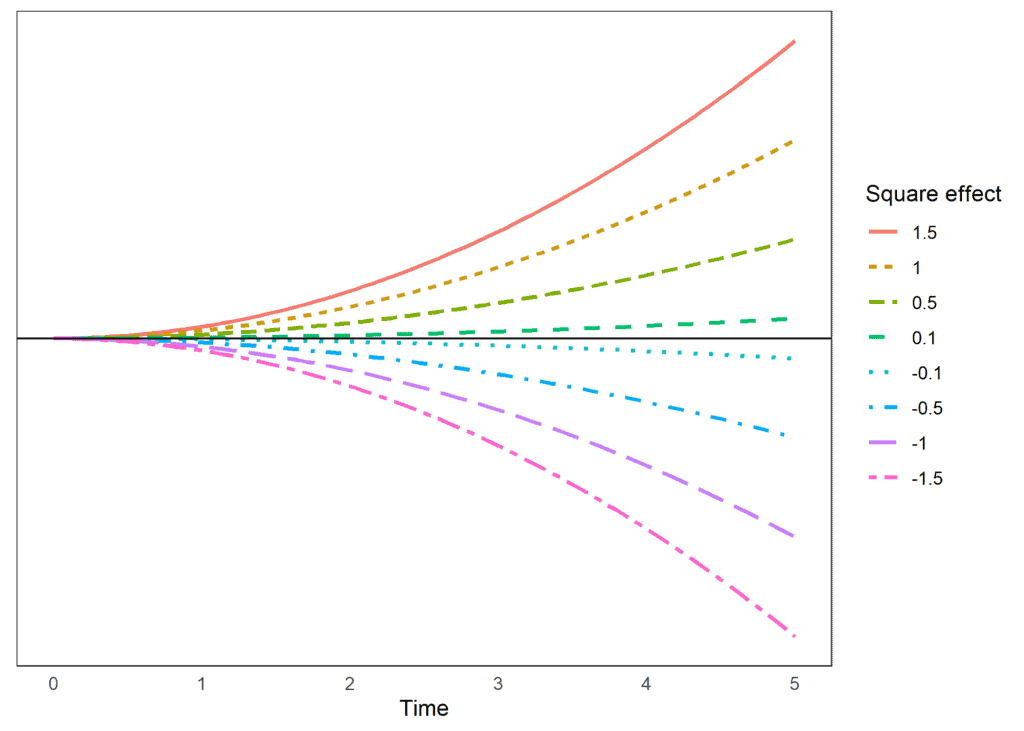
We can also look at some hypothetical examples that include a cube effect. Again, the main effect is 0, so it would indicate no trend. However, the combination of square and cube effects allows for different trends in time.
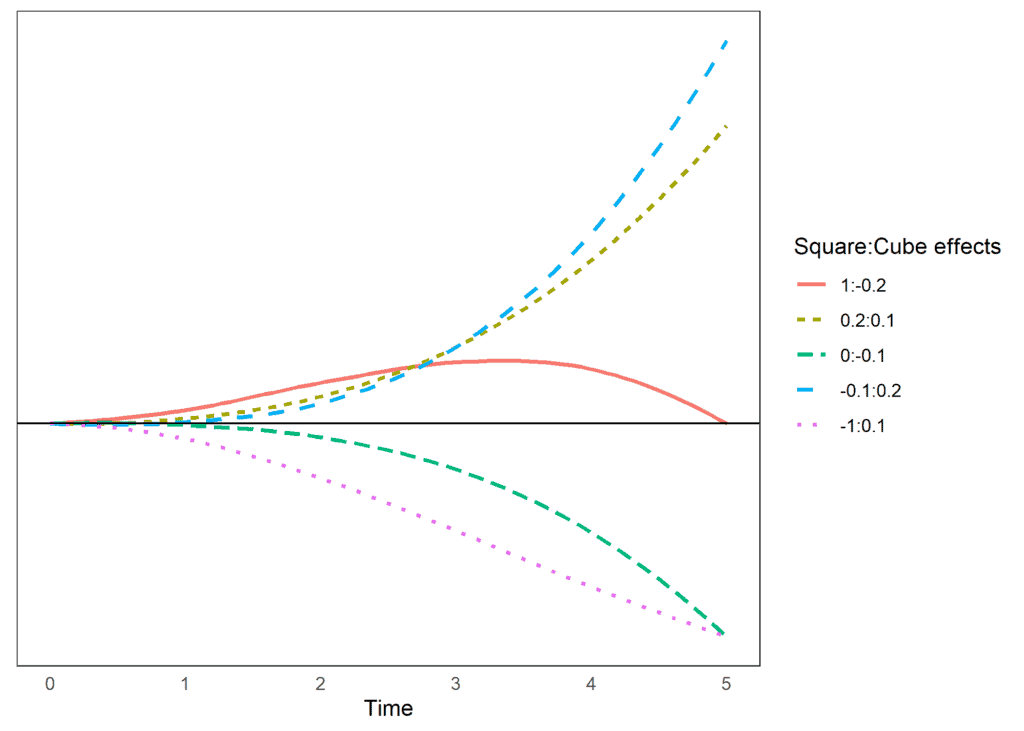
If we look at the situation when the square effect is 1, and the cube has an effect of -0.2, we see an initial upward trend and then a decrease, reaching 0 by wave 5. If both the square and the cube are positive, we will see an accelerated trend that increases as time passes. We also see that we can reach similar estimates in wave 5 with different change patterns. For example, both having a square effect of -1 and a cube effect of 0.1 and having a square effect of 0 and a cube effect of -.1 reach a similar point in wave 5, but if we continue that trend, the trajectories would become quite different.
Let’s look at the linear model so we can use it as a reference (for an in-depth interpretation of the coefficient, check this post).
m2 <- lmer(data = usl, logincome ~ 1 + wave0 +
(1 + wave0 | pidp))
summary(m2) ## Linear mixed model fit by REML ['lmerMod']
## Formula: logincome ~ 1 + wave0 + (1 + wave0 | pidp)
## Data: usl
##
## REML criterion at convergence: 98116.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -7.8825 -0.2306 0.0464 0.3206 5.8611
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## pidp (Intercept) 0.69590 0.8342
## wave0 0.01394 0.1181 -0.51
## Residual 0.21052 0.4588
## Number of obs: 52512, groups: pidp, 8752
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 7.057963 0.009598 735.39
## wave0 0.041934 0.001723 24.34These results imply that income increases linearly by 0.04 for each wave. We can add the polynomials to the model if we believe there are non-linear effects. For example, we can include the square effect using this code:
m2_sq <- lmer(data = usl, logincome ~ 1 + wave0 + wave_sq +
(1 + wave0 | pidp))
summary(m2_sq)## Linear mixed model fit by REML ['lmerMod']
## Formula: logincome ~ 1 + wave0 + wave_sq + (1 + wave0 | pidp)
## Data: usl
##
## REML criterion at convergence: 98073.4
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -7.9234 -0.2301 0.0478 0.3199 5.8314
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## pidp (Intercept) 0.69607 0.8343
## wave0 0.01396 0.1182 -0.51
## Residual 0.21019 0.4585
## Number of obs: 52512, groups: pidp, 8752
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 7.0381081 0.0099629 706.428
## wave0 0.0717158 0.0043647 16.431
## wave_sq -0.0059563 0.0008021 -7.426
Looking at the fixed effects for the linear and the square of time, we observe an initial positive slope (0.07) followed by a negative square effect (-0.01). As such, we would expect an initial increase in log income and then a decrease.
We can also compare the predicted scores from the model that assumes linear change and the model that also includes square effects against the observed average. It appears that the square effect fits the observed data better, albeit not perfectly.
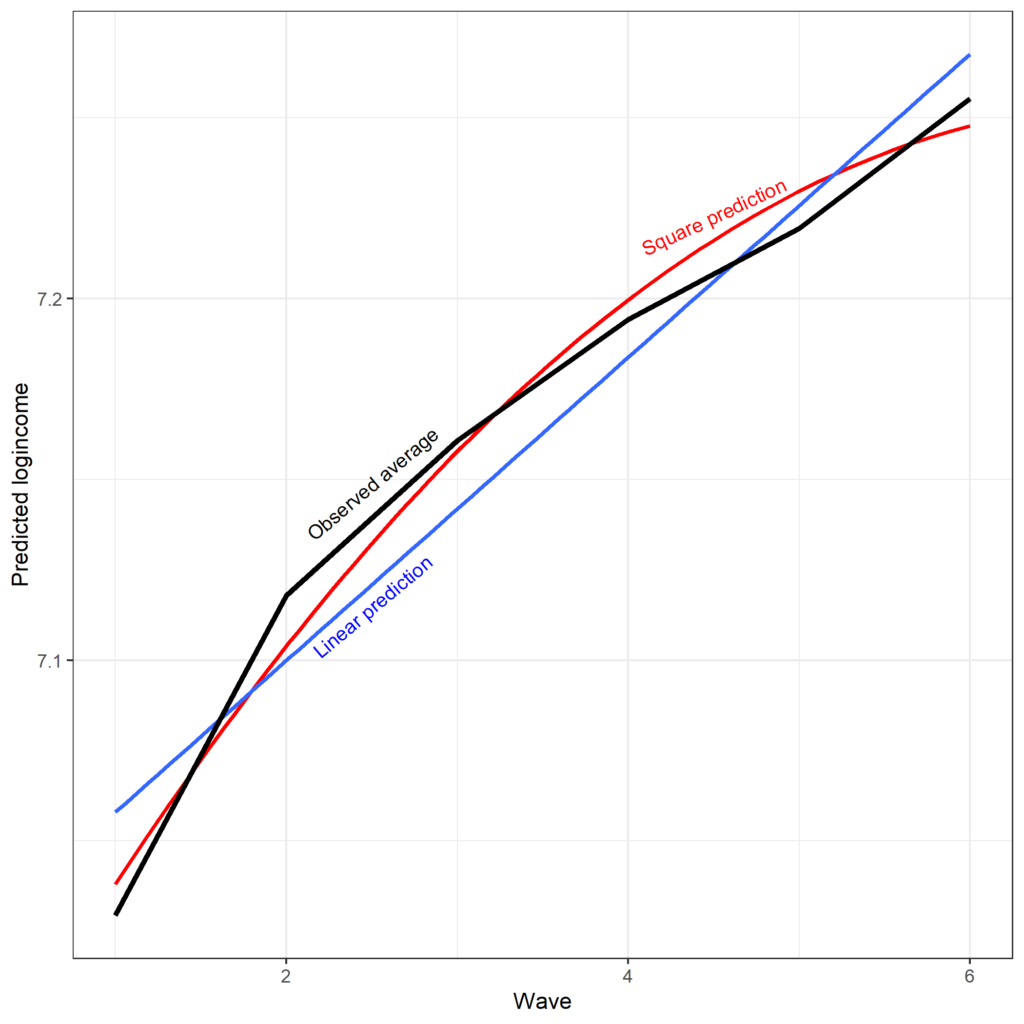
One thing to note about the previous non-linear model is that we did not include the square effect in the random part of the model. This means that the non-linear bend in time is the same for everyone. We can free that assumption by including the square time in the random part of the model, thus allowing each individual to have their own non-linear trend. While this is typically a more realistic assumption, this model can be complex and lead to estimation issues, depending on the outcome and the number of cases and waves. For example, this model does not work for our current data but would estimate if we used 11 waves of data.
m2_sq_re <- lmer(data = usl_all, logincome ~ 1 + wave0 + wave_sq +
(1 + wave0 + wave_sq | pidp))
summary(m2_sq_re) ## Linear mixed model fit by REML ['lmerMod']
## Formula: logincome ~ 1 + wave0 + wave_sq + (1 + wave0 + wave_sq | pidp)
## Data: usl_all
##
## REML criterion at convergence: 883956.3
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -7.0310 -0.1406 0.0725 0.2895 5.5940
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## pidp (Intercept) 1.6890306 1.29963
## wave0 0.0987768 0.31429 -0.63
## wave_sq 0.0007027 0.02651 0.43 -0.92
## Residual 0.6234185 0.78957
## Number of obs: 306953, groups: pidp, 50994
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 6.6498507 0.0064688 1027.98
## wave0 0.1218175 0.0022977 53.02
## wave_sq -0.0079053 0.0002277 -34.72We observe again an initial positive trend and then a negative square effect when we use 11 waves, as when we analyzed only 4. If we sample a few cases and plot the predicted scores, we can see the model-implied trends and capture some of the individual variation present due to the random effect of the square effect.
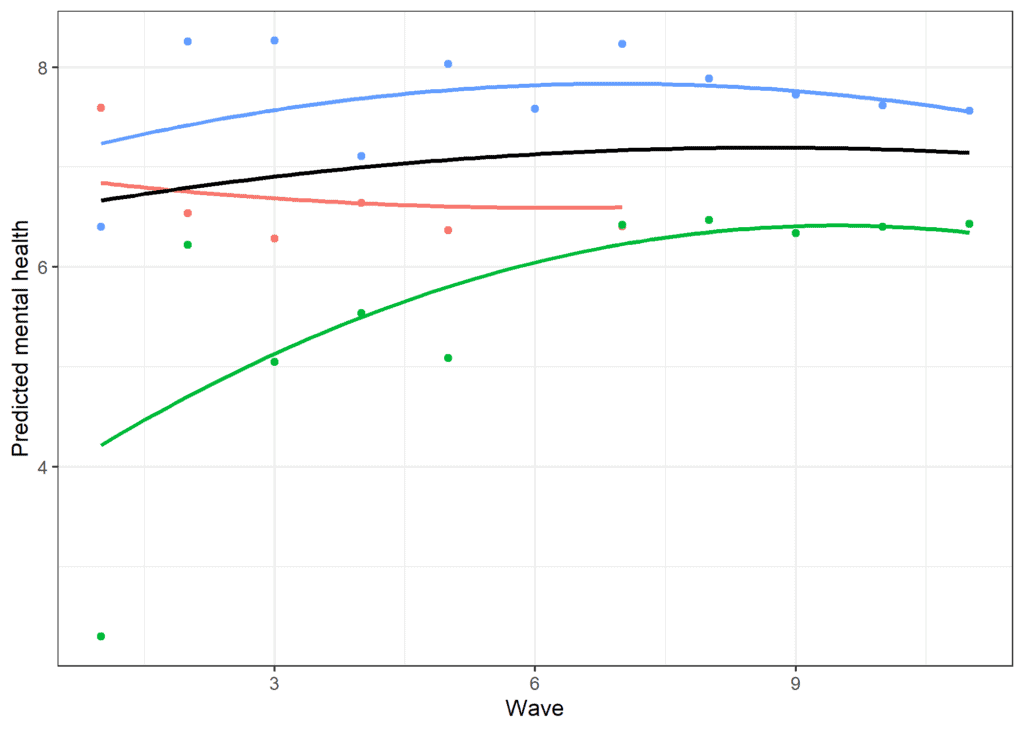
Nonlinear change in time using a categorical variable
An alternative way to model non-linear change is to treat time as a discrete/categorical variable. In that case, we can estimate the expected value of the outcome at each point in time or in a particular range of time. The most general approach treats each time point as a discrete variable. While this doesn’t make any assumptions about the shape of the change in time, it is a complex model that may have estimation problems.
To try this out with our model, we can define the time variable as a factor. By default, lmer() (like the lm() command) transforms factors into dummy variables and treats the first category as the reference. We can use this to model non-linear change.
usl <- mutate(usl,
wave_fct = as.factor(wave))We can now include this in our model.
m2_dummy <- lmer(data = usl, logincome ~ 1 + wave_fct +
(1 + wave0 | pidp))
summary(m2_dummy) ## Linear mixed model fit by REML ['lmerMod']
## Formula: logincome ~ 1 + wave_fct + (1 + wave0 | pidp)
## Data: usl
##
## REML criterion at convergence: 98071.9
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -7.9319 -0.2313 0.0482 0.3210 5.8448
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## pidp (Intercept) 0.69611 0.8343
## wave0 0.01397 0.1182 -0.51
## Residual 0.21009 0.4584
## Number of obs: 52512, groups: pidp, 8752
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 7.029381 0.010176 690.81
## wave_fct2 0.088438 0.007043 12.56
## wave_fct3 0.131348 0.007375 17.81
## wave_fct4 0.164791 0.007898 20.86
## wave_fct5 0.190032 0.008576 22.16
## wave_fct6 0.225894 0.009376 24.09Notice that we still treat the random part of the model linearly. Again, estimating a random effect at each wave can lead to issues with model estimation, so we use a simplified random effect.
Using this model, we can calculate the expected mental health at each point in time. The intercept again refers to the predicted value at the beginning of the study as that is the reference or missing category. The expected value is 7.03. To get the expected value for wave two, we add the intercept and the effect of wave 2: 7.03 + 0.09 = 7.11. We can use a similar approach for waves 3 and 4. We can also compare the results from this model with the observed scores and the predictions from the square model.
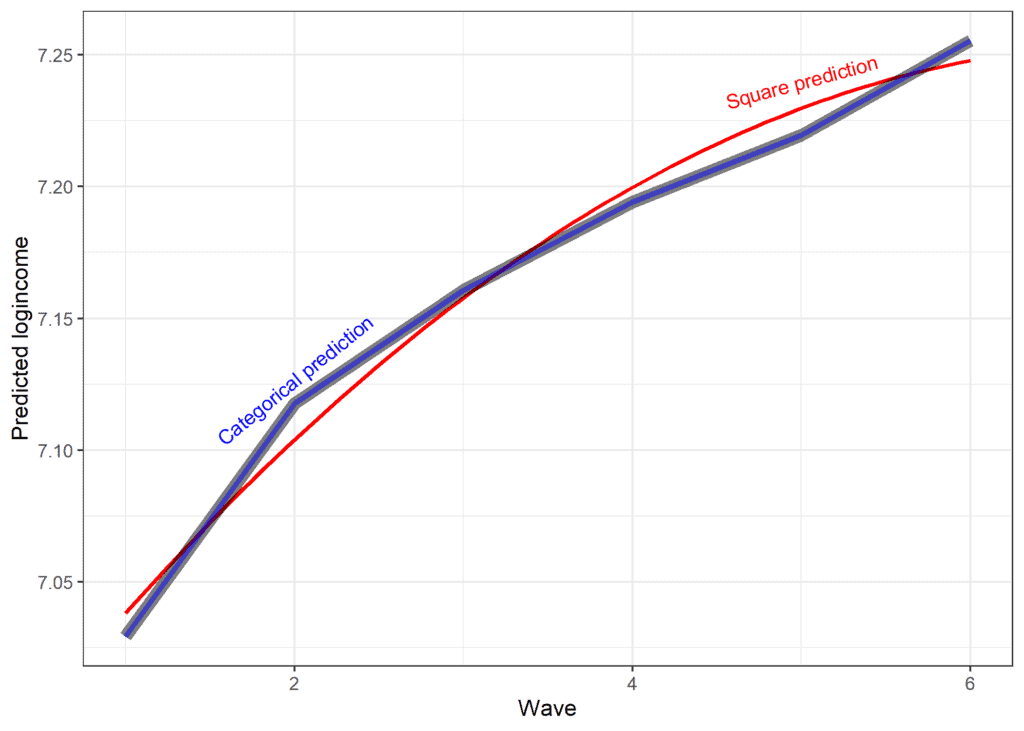
The new prediction is almost identical to the observed data (lines overlap). That being said, there is a trade-off between the model’s simplicity and how well it explains the data. We can formally compare the different models we estimated to decide how to treat the change in time for log income.
anova(m2, m2_sq, m2_dummy)
## Data: usl ## Models: ## m2: logincome ~ 1 + wave0 + (1 + wave0 | pidp) ## m2_sq: logincome ~ 1 + wave0 + wave_sq + (1 + wave0 | pidp) ## m2_dummy: logincome ~ 1 + wave_fct + (1 + wave | pidp) ## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq) ## m2 6 98109 98163 -49049 98097 ## m2_sq 7 98056 98118 -49021 98042 55.108 1 1.141e-13 *** ## m2_dummy 10 98043 98131 -49011 98023 19.629 3 0.0002026 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
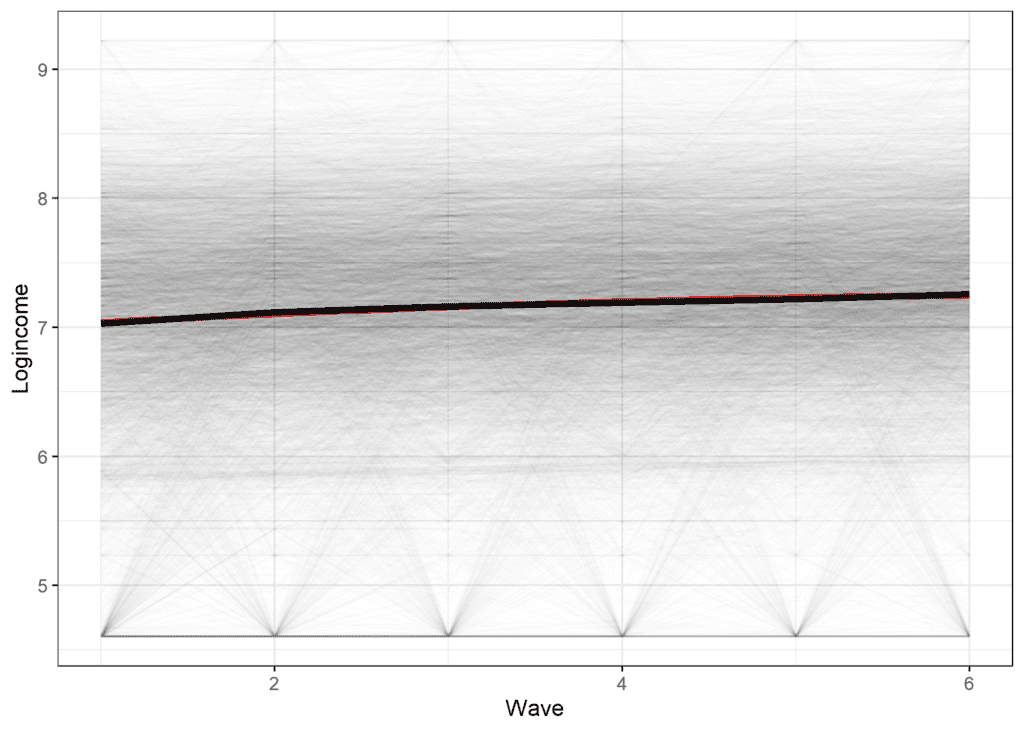
Based on the AIC and the Chi-square, we should select the final model, where we treat time as categorical, while based on BIC, we should choose the model using square effects. The graph below shows that while the square effect (red line) does not perfectly represent the actual average (black line), it is relatively close given the amount of variability in the data (the thin lines represent the scores of different individuals).
Conclusions
Hopefully, this will give you an idea of how the multilevel model for change can be expanded to include non-linear effects. Other, more complex trends can be estimated using models such as splines (an introduction here). The model can also include time-constant predictors, as discussed here. You can also compare this approach with modelling non-linear effects using Latent Growth Models.
Was the information useful?
Consider supporting the site:
