In a previous post, we discussed the multilevel model for change, which investigates average change in time while accounting for individual-level variation. In this blog post, we will discuss how to extend this model to include predictors.
Time-varying versus time-constant variables
When working with longitudinal data, we can consider variables to be time-varying or time-constant. For example, a survey measure of general satisfaction is a time-varying variable as it is collected in each wave. So, for each individual, this could change (although it does not have to change). The year of birth is a time-constant variable. Collecting this information once from each individual is enough, as we do not expect it to change.
There are also some situations where we can treat a variable as time constant or time-varying. For example, we could recode birth year as age, a time-varying variable. Similarly, we could take each individual’s average of general satisfaction and make that variable time constant. In such situations, treating a variable as time-constant or variable should be based on theoretical considerations, our data and the modelling strategy used. You can read more about this in the post about data structures.
Explaining Change
Here, we will expand the multilevel model to include time-constant predictors. In a previous post, we explored how best to describe the change in time of the outcome by including non-linear effects. This is an essential first step in analyzing longitudinal data. Nevertheless, we often want to understand the causes of that change or at least how different groups may have different rates of change. We will turn to this aspect, discussing the inclusion of time-constant predictors and the same Understanding Society data.
Including Time Constant Predictors
We will start by adding a time-constant predictor to our model. For example, let’s explore how the change in mental health is different for men and women (where we treat these as time constant). If we add the “gndr” variable to our model, the new formula for our regression will be:
Yij = γ00 + γ01GNDRi + γ10TIMEij + ξ0i + ξ1iTIMEij + ϵij
The interpretation of the coefficients is mostly the same as before. The interpretation of the intercept (γ00) changes and now refers to the expected value of the outcome when “gndr” and “time” are 0. In our case, this would refer to males at the beginning of the study. The effect of “gndr” (γ10) refers to how different females are from males in their mental health. The interpretation of the random effects is the same as before.
We will use the linear change in time model to keep things simple, but this can be easily expanded to include non-linear change.
Let’s run this model:
m3 <- lmer(data = usl, sf12mcs ~ 1 + wave0 + gndr +
(1 + wave0 | pidp))
summary(m3)## Linear mixed model fit by REML ['lmerMod'] ## Formula: sf12mcs ~ 1 + wave0 + gndr + (1 + wave0 | pidp) ## Data: usl ## ## REML criterion at convergence: 669722 ## ## Scaled residuals: ## Min 1Q Median 3Q Max ## -6.0382 -0.4070 0.1166 0.5036 4.6337 ## ## Random effects: ## Groups Name Variance Std.Dev. Corr ## pidp (Intercept) 52.552 7.249 ## wave0 2.915 1.707 -0.25 ## Residual 40.841 6.391 ## Number of obs: 94435, groups: pidp, 26769 ## ## Fixed effects: ## Estimate Std. Error t value ## (Intercept) 51.71612 0.07857 658.22 ## wave0 -0.41987 0.02139 -19.63 ## gndrFemale -1.96590 0.09727 -20.21 ## ## Correlation of Fixed Effects: ## (Intr) wave0 ## wave0 -0.365 ## gndrFemale -0.700 -0.001
We will concentrate on interpreting the fixed part of the model. As mentioned before, the intercept (51.72) represents the expected mental health at the beginning of the study. The effect of “wave0” (-0.42) refers to the rate of change in mental health, as before. This effect is the same both for men and women. Finally, the effect of “gndr” (-1.97) indicates how females are different to men or mental health. In our data, it appears that they have lower mental health on average.
This model can include multiple time constant predictors of different nature, categorical or continuous. The interpretation will be the same as in a regular regression.
Allowing for different rates of change
One crucial assumption we made so far is that the rate of change is the same for men and females. That means that the difference in mental state remains constant in time. This is often an important question that we want to explore. From a substantive point of view, having different rates of change, which would lead to convergence or divergence, is very important. To explicitly examine this in our model, we can add an interaction between gender and time. This would allow for different rates of change for men and women. We would write this model as follows:
Yij = γ00 + γ01GNDRi + γ10TIMEij + γ11GNDRi * TIMEij + ξ0i + ξ1iTIMEij + ϵij
We can easily include interactions in lmer() by adding the two variables separated by :. So our new model is:
m4 <- lmer(data = usl, sf12mcs ~ 1 + wave0 + gndr + gndr:wave0 +
(1 + wave0 | pidp))
summary(m4)## Linear mixed model fit by REML ['lmerMod'] ## Formula: sf12mcs ~ 1 + wave0 + gndr + gndr:wave0 + (1 + wave0 | pidp) ## Data: usl ## ## REML criterion at convergence: 669726.4 ## ## Scaled residuals: ## Min 1Q Median 3Q Max ## -6.0380 -0.4067 0.1166 0.5035 4.6335 ## ## Random effects: ## Groups Name Variance Std.Dev. Corr ## pidp (Intercept) 52.551 7.249 ## wave0 2.915 1.707 -0.25 ## Residual 40.841 6.391 ## Number of obs: 94435, groups: pidp, 26769 ## ## Fixed effects: ## Estimate Std. Error t value ## (Intercept) 51.710221 0.085255 606.535 ## wave0 -0.415472 0.032649 -12.726 ## gndrFemale -1.955542 0.113295 -17.261 ## wave0:gndrFemale -0.007702 0.043216 -0.178 ## ## Correlation of Fixed Effects: ## (Intr) wave0 gndrFm ## wave0 -0.514 ## gndrFemale -0.753 0.387 ## wv0:gndrFml 0.388 -0.755 -0.513 ## optimizer (nloptwrap) convergence code: 0 (OK) ## Model failed to converge with max|grad| = 0.00590502 (tol = 0.002, component 1)
When we have interactions in a regression model, we must be careful how we interpret the main effects. In our results, the interpretation of the intercept stays the same (the expected value at the beginning of the study for men is 51.71), but the interpretation of the other coefficients is different. The effect of time (-0.415) now refers to the rate of change in mental health for men, and the effect of gender (-1.96) now refers to the difference in mental health at the beginning of the study. These two interpretations are due to the interaction effect that we now have in our model. This final coefficient (-0.008) can be interpreted as how different is the rate of change for females compared to men. To get an exact size, we can get the rate of change for men (-0.415) and add it to the interaction effect (-0.008), leading to a rate of change for females (-0.423). This would indicate that mental health is deteriorating at a slightly faster pace for females compared to men. Given that females start with lower mental health (-1.96), this implies that, in time, the two will become even more different. That being said, the effect of the interaction is relatively small.
We can also see this visually by using the predicted scores:
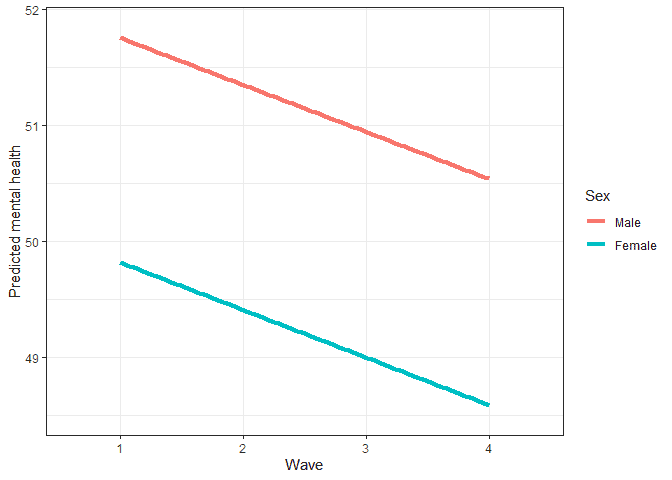
Men start with higher mental health values in line with the intercept coefficient. The two lines showing the change in time for men and women look almost parallel, highlighting that the interaction effect is relatively small here.
We can expand the model to see an important example of interaction effects. Below, we include the effect of degree, another variable we treat as a time constant, as well as the interaction with time. Given the small effect we observed earlier, we keep the main effect of sex but exclude the interaction with time.
m5 <- lmer(data = usl, sf12mcs ~ 1 + wave0 + gndr +
degree + degree:wave0 +
(1 + wave0 | pidp))
summary(m5)## Linear mixed model fit by REML ['lmerMod'] ## Formula: sf12mcs ~ 1 + wave0 + gndr + degree + degree:wave0 + (1 + wave0 | ## pidp) ## Data: usl ## ## REML criterion at convergence: 669330.5 ## ## Scaled residuals: ## Min 1Q Median 3Q Max ## -6.0343 -0.4070 0.1157 0.5045 4.6426 ## ## Random effects: ## Groups Name Variance Std.Dev. Corr ## pidp (Intercept) 52.35 7.236 ## wave0 2.91 1.706 -0.25 ## Residual 40.83 6.390 ## Number of obs: 94391, groups: pidp, 26751 ## ## Fixed effects: ## Estimate Std. Error t value ## (Intercept) 52.34373 0.10892 480.580 ## wave0 -0.50243 0.03546 -14.170 ## gndrFemale -1.96869 0.09720 -20.255 ## degreeNo degree -0.97285 0.11714 -8.305 ## wave0:degreeNo degree 0.12863 0.04446 2.893 ## ## Correlation of Fixed Effects: ## (Intr) wave0 gndrFm dgrNdg ## wave0 -0.443 ## gndrFemale -0.505 -0.001 ## degreeNdegr -0.693 0.412 0.001 ## wv0:dgrNdgr 0.353 -0.798 0.000 -0.513 ## optimizer (nloptwrap) convergence code: 0 (OK) ## Model failed to converge with max|grad| = 0.0233356 (tol = 0.002, component 1)
Now, the intercept (52.34) refers to the expected mental health in wave 1 for men with a degree. At the beginning of the study, it appears that participants without a degree have lower levels of mental health (-0.97). And while mental health is deteriorating with the passage of each wave (-0.5), this is happening at a lower rate for those without a degree (0.13), implying a convergence. Again, we can use the predicted scores to see this more clearly in a graph:
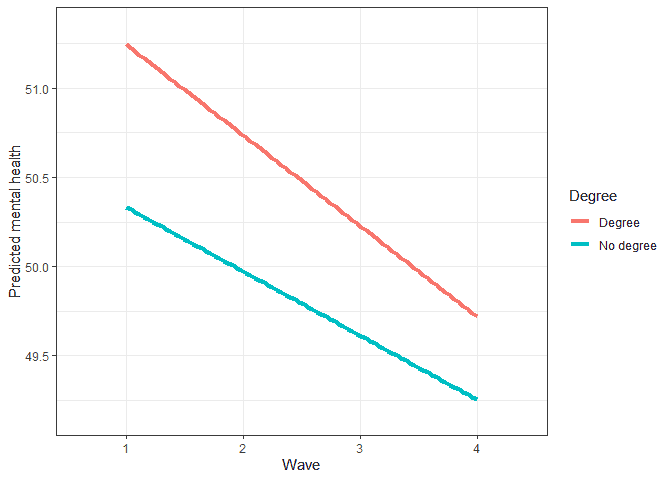
Conclusions
The multilevel model for change can be easily expanded to include time-constant predictors. For the most part, the interpretation is similar to that from multiple regression. Care is needed with the interpretation when including interactions with time to allow for different rates of change for subgroups. You have seen above some example code for using predicted scores and visualizations to better understand your model’s results. You can also check how to include time varying predictors in this blogpost as well as investigating nonlinear change in time here.
Was the information useful?
Consider supporting the site:
